【エンジニアはやっている】ビジネスに使える課題へのアプローチ・解決法
課題の多い社会
社会には課題が山積みです。規模がかなり大きいですが、文部科学省にこんな資料もありました。『経済・社会的な課題への対応』
でもなぜこんなに課題が多いのでしょうか?
特に日本は、少なくとも中学校までは卒業する人が殆どなので、
しっかりと教育を受けた良識のある大人が多いはずです。それなのに。
ただ実際には人間関係の問題、環境問題、国や地域レベルの問題、教育の問題、医療の問題、人権の問題などなど 枚挙に暇がありません。
私達はそんな課題の多い社会で、ことの大小はあれど、その課題を解決していくことが求められていると思っています。
となると、課題の解決方法がないといけませんよね。今回は、そんな課題の解決アプローチを4つ紹介していきます。
バイナリサーチ(2分探索法)
このアプローチは知っていますか?
Weblio辞書によると、以下のようになっています。
2分探索法とは、検索対象がソートされている場合に適用できる高速な検索手法のことである。
2分探索法は、具体的には次のようなアルゴリズムで検索を行う。まず、検索の開始は、真ん中に位置するデータと比べる。一致すればそれで終わりである。小さければ目的のデータは前半にあり、大きければ後半にある。これをデータが無くなるまで繰り返す。
この手法の胆は、検索範囲を2分割することで、検索対象が一気に絞り込まれるところにある。1000個のデータに対しては多くても10回程度の比較により結果が得られる。一般にN個のデータから検索する場合にはlog2N回のオーダーの比較で目的とするデータが得られる。
エンジニアがよく取るアプローチなのですが、つまり課題を見つけるため、対象を半分ずつチェックして特定をしていくようなアプローチです。
例えば、何かの実装を行ったところ、エラーになってしまった。その時にエラーの原因を特定したい。対象ソースが1000行とすると、まずは1〜500の間なのか、501〜1000の間なのかを特定する。仮に1〜500の間だとわかった場合は、問題が今度1〜250の間なのか、251〜500の間なのかを特定する。そうやって繰り返していくことで原因を特定していくアプローチです。
リニアサーチ(線形探索法)
これは、上からデータをひとつずつチェックして探索していく方法です。 探索する量が膨大だと果てしなく探す時間がかかってしまうため問題なのですが、 網羅的に、MECEに探索ができるため、課題解決のアプローチとしてはバイナリサーチと同様に重要なものです。
分解
デカルトは「困難を分割せよ」と言い、ビル・ゲイツは「問題を切り分けろ」と言ったそうです。
ハフポストの記事を見ると、ビル・ゲイツの話が載っています。お客さんがMicrosoftの技術的な問題でたいそう怒っている状況でビル・ゲイツは問題を分解しました。すると、当初問題だと思われていた技術的な問題はクライアントの怒りとは独立した問題で、実際には担当者との性格不一致ということがわかりました。普通に問題に立ち向かっていたらおそらくどうやっても分からなかった事が判明し、そこを対処して困難を乗り切ったそうです。
問題を素直にそのまま捉えて「う〜ん...」とやっていても埒が明きません。
そこで、問題を分解して小さな単位に分けていきます。すると、大きな問題を構成している要素は案外単純なものです。
√2 分解複眼アプローチ
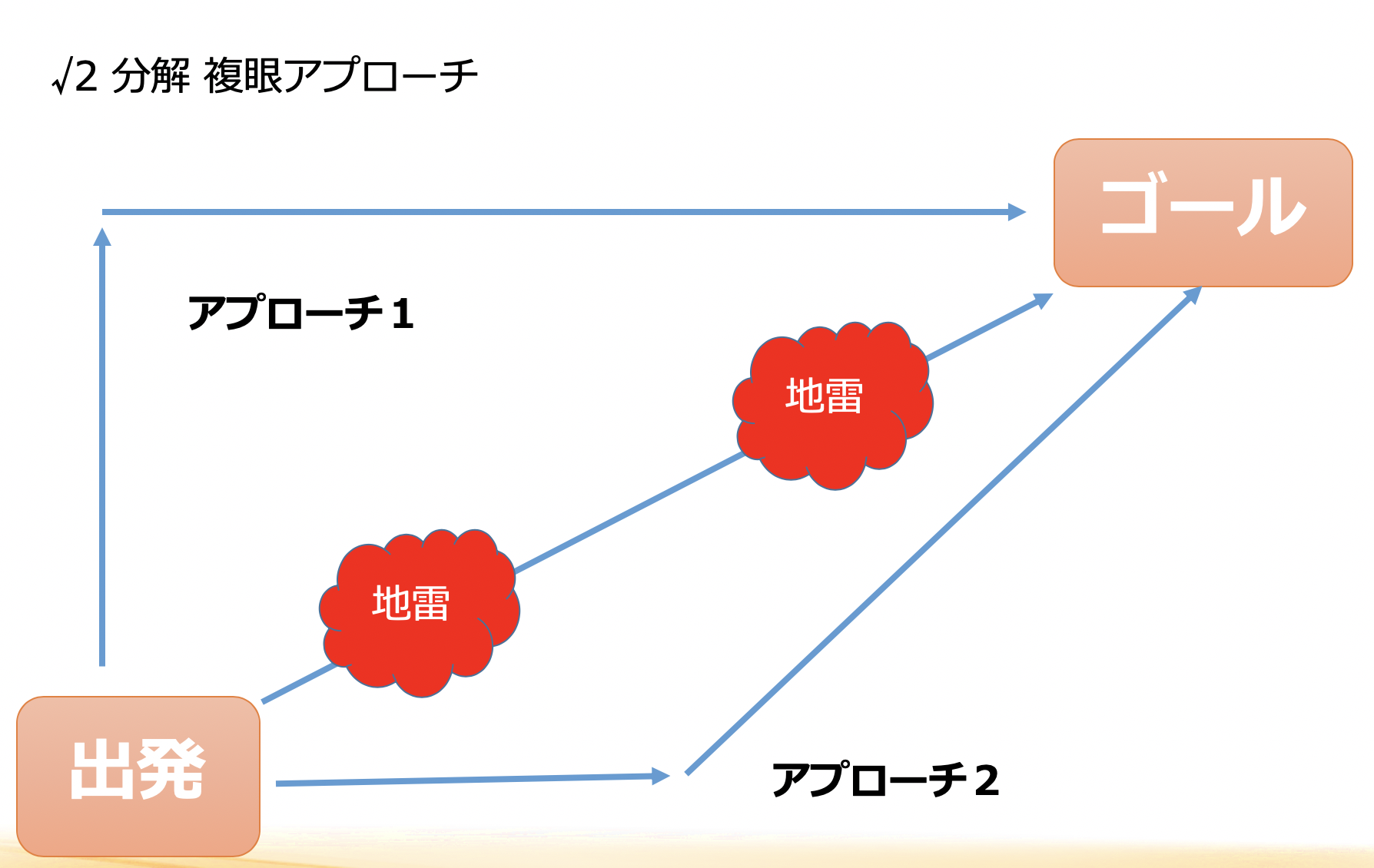
問題解決の出発点からゴールまで、最短で進めたいと思うのは当然のことです。しかし、これが危険なのです。最短でやる場合、そこには地雷が埋まっているものだと頭の隅っこに置いておくことも大事です。そこで、√2。ルートは数学で習ったことがあるかと思いますが、思い出してみると直角二等辺三角形のそれぞれの辺の長さの比率は、1 : 1 : √2 です。
√2 = 1.41421356237 なので、上の図で言うアプローチ1をとった場合、 1 + 1 = 2 となりますので、√2 を通るのが最短となります。
しかし長期的に見ると、アプローチ1のような進み方をするほうがうまくいくのです。理由としては、地雷処理をしながら進む時間、とりわけ地雷が爆発した際のリカバリーをする時間が恐ろしく膨大にかかるためです。
急がば回れということですね。
まとめ
今回は、エンジニアは必須で知っておくべき課題解決法でおそらく汎用的に使えるであろう方法を書いてきました。
エンジニアではなくとも、普段のビジネスにおいてもこういう課題解決のアプローチを多く知っておくことで解決の手立てがつきやすく、自らのパフォーマンスも向上します。
課題解決のベクトルが自分に向いていようが、お客さんに向いていようがかかわらず考え方として大事にしたいものばかりを書いてみました。
私、穂苅智哉の情報は、以下のFacebookページTwitterアカウントを御覧ください!
※友達申請をいただける方は、お手数ですがメッセージを添えておねがいいたします。