2桁の掛け算を斜め線で簡単に計算する方法を視覚化してみる

» 2013/01/22

　こんにちは。わかりにくい解説をわかりやす～く組み替える職人の開米瑞浩です。

　今日は珍しく（？）、本職に近い話です。昨日ネットでふと目にとまったある算数ネタについて書いてみることにしましょう。

　なんでも「斜めに線を引いて交点を数えるだけで掛け算が簡単に計算できる、すごいね！」というもので、こういう方法です。
　　　 　　　


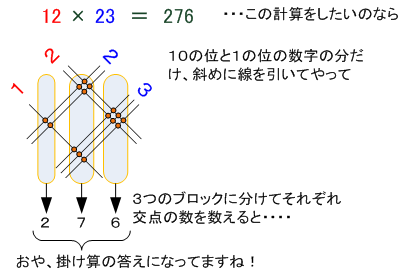
　筆算で繰り上がりの処理をする手順を覚えなくても、「数え上げ」だけで答えが出るわけです。　昨日、twitterやfacebookで私が見ているTLでこれが話題になっていたのですが、この方法、計算テクニックというよりも「数」の性質を勉強するためのひとつの小ネタ（小学生向きです）としておもしろいところがあるので、ちょっと書いてみようと思いました。（ちなみに、この手法は3桁以上の掛け算にも使えますが、数の組み合わせによってはかえってめんどくさくなったりするので万能ではありません）

　まずは、

　　なぜこういう手順で正しい答えが出るのか？

　が一目でわかるように視覚化してみましょう。
　それには、図をちょっと変えてこんな風に書きます。

 　　　　


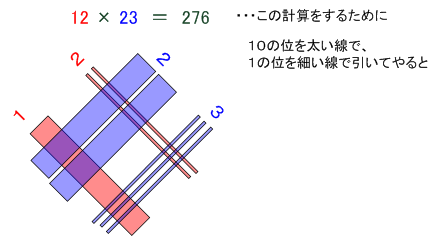
　これの意味をもう少しわかりやすくするために、「線が交わった」部分だけを残して他を消すとこんなふうになります。



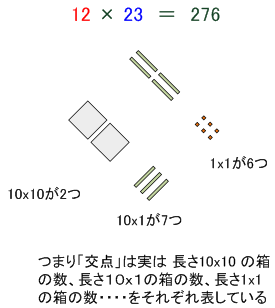
　というわけで、「交点」は実は面積１００，１０，１にそれぞれ規格化された箱のことを意味していたわけです。

　こう考えれば「斜めの線を引いて交点を数える」というのが何をやっているのか直感的にわかるというものですが、これで終わらせるのももったいないのでもう一歩進めましょう。上の図で残した「10x10、10x1、1x1」のそれぞれの箱を全部組み合わせると・・・・・

 


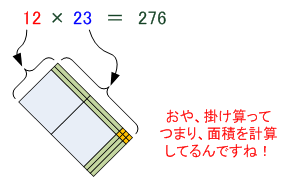
　こんなふうに、「交点」を箱で表してやると、それを組み合わせることで「長方形」になります。こうすれば、「掛け算というのはつまり、面積を計算しているんだ」ということが直感的にわかりますね。

　と、いうわけです。斜めに線を引いて交点を数えれば掛け算の答えが出る、というのは確かに事実ではありますが、それを単に計算テクニックとして覚えるだけではもったいない、と私は思うのでした。