『ザ・ベロシティ』のサイコロのゲームをやってみた　２　〜制約前の予測不能なダブツキ在庫〜

　昨日に引き続き、ＴＯＣ理論ものの王道の『ザ・ゴール』シリーズの『ザ・ベロシティ』で紹介されている工程のラインバランスをイメージしたサイコロのゲームに触れていきたいと思います。

　ちなみに、昨日のブログは、こちら

　昨日は、各工程の生産指示を正七面体（実際にはありえませんが）のサイコロを振るかの如くその量を決めてみました。工程前に滞留する仕掛品の量が、生産指示より少ない場合には無論、仕掛品の在庫量しか生産は出来ず、次工程への払い出しもその量となります。

　同著では、次に、各工程の生産指示の量をサイコロ２つ振ってその出目としています。しかし、１つの工程のみ制約として、サイコロ１つ振ることとしています。背景には、大多数の生産設備の能力を２倍にするということではなく、無理に生産能力を削ぎ落とすことのないような状態をやや大げさにイメージしたものと思います。

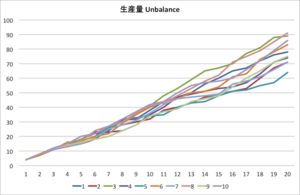
　私のほうでは、工程をＡ〜Ｇまでの７つの工程としましたので、制約を設けた工程は真ん中となる４番目のＤ工程としました。大多数の工程では、サイコロ（ありえない正七面体）を２つ振りますので期待値は８となります。２０日稼働ですので、制約がなければ、１６０は期待したいとざっくり感じるかもしれません。

　生産量ですが、１０回の試行で最小で６４最大で９１で平均は約７８（８７は誤植でした。すみません。）といったところでした。

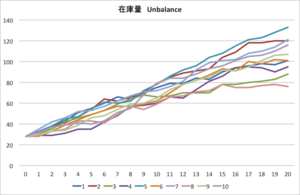
　在庫量は最小７６最大１２１で平均は約１０６と、初期の在庫量の約３．８倍に膨らんでしまいました。

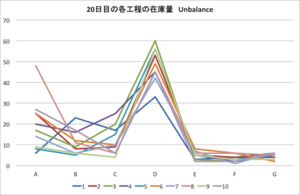
　興味深い点ですが、２０日経過後の各工程の在庫量です。制約とした工程Ｄの在庫量が多くなっていることが一目瞭然ですが、制約の前工程である工程Ａ〜Ｃについては仕掛品のダブツキが見られ、そのダブツキが工程Ａ〜C内において上流寄りに起こるのか下流寄りに起こるのかは一定しません。

　要するに、制約となる工程の上流では、仕掛品のダブツキが生ずるもののその予測は困難となることが推察されるでしょう。

　次回は、最後として、ＴＯＣ理論のＤＢＲ（ドラム・バッファー・ロープ）のイメージに近い状態に触れていきたいと思います。