『ザ・ベロシティ』のサイコロのゲームをやってみた　１　〜ＴＯＣ理論が指す意味あるムダのざっくり感〜

　読んでみただけでは、「へぇ〜」と思うことでも、もう少し手を動かすと「へぇ〜」もより深みが増すことかと思います。

　もはやＩＴとものづくりは切り離せない関係にあり、メーカーの生産技術としてＩＴに深く携わっている方も多いことと思います。私自身も、出は生産技術系の社内ＳＥですので、比較的プロセス管理ものについても、いつも関心を持っています。

　昨年の秋に出た本なので、ちょっと古めの話になってしまうかもしれませんが、ＴＯＣ（制約理論）の定番中の定番『ザ・ゴール』シリーズの新刊として『ザ・ベロシティ』が出版されました。
　徹底した無駄を削ぎ落としラインのばらつきを減らし平準化をはかるリーン系の生産方式に対して、現実問題として、多くの中小企業では顧客からの要求への対応として投入量も主導的にコントロールすることは難しいのが現状かと思います。時間を掛けて究極のラインバランスを追い求めるも、内外の要因含めて変動はつきものでしょう。
　現場のマネージャにもなると、時として自部門への関心が高くなり、推進した部分最適化も全体としては、なかなかパフォーマンスがあがらないことも多々あることでしょう。（私も、かつてそんなジレンマを感じることもおおくありました。）

　この本では、リーン系の批判ではなく、現実にある「ばらつき」を許容／考慮すべき点と、よい部分はよいものとして取り入れましょうとの２つのメッセージが込められているかと思います。

　同著の中で、ＴＯＣの事例を示すサイコロを使ったシミュレーションが出てきます。このシミュレーションは、同著にて２回ほど、各数ページにわたり紹介されています。
　加工処理順序を持つ生産ラインにて、理想的にラインのキャパシティと投入量がコントロールされている環境ではなく、投入量とキャパシティのばらつきを想定したラインとして、各工程で処理できる量のばらつきをサイコロの出目に見立て、ラインとしての生産量と在庫量をシミュレートしています。

　実際に手を動かしてみないと分からないこともあるので、自分でも表計算ソフトで少しシミュレートしてみました。

　工程Ａ〜工程Ｇまで７つの工程を想定します。まず、同著にならい、各工程の初期在庫を４とします。各工程の１日の生産指示ですが、同著ではサイコロの出目としているので１〜６ですが、期待値が３．５になってしまうのは少し気持ち悪いので、１〜７の乱数としてみました。また、１月をイメージするために２０日稼働を想定してみました。

　究極のラインバランスが取れていると仮定すると期待値の４が１日の処理量です。工程Ａでは在庫量４があるので、１日の処理量の４を次工程の工程Ｂへ払い出すことができ、同時に、生産計画の部門からラインへの投入も４として工程Ａに４が投入されるとします。以下、同様に工程は進み、さすれば、最終工程となる工程Ｇからは、生産量４が発生することでしょう。結果的に、１ヶ月にて、８０（４×２０日）が生産されることと思います。

　今回設定したばらつきにて、各工程にて在庫量以上の生産指示となる場合もあるでしょう。その際には、在庫量しか処理はできないこととなり、その後、前工程から払い出された量（いわば、仕掛品）が加算されることとなります。（このあたり、詳しくはこの本をお読みいただけると良いと思います。）

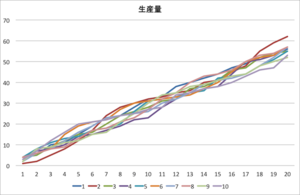
　さて、シミュレートしてみました。シミュレートは、１０回の試行としてざっくり、振る舞いかげんも見てみましょう。やはり、グラフ等見える形で表現すると気付きもあることと思いますので。

　生産量は、同著の通り期待値通りとはなりませんでした。１０回の試行の平均にて５６となり期待値の７割程度ということになります。

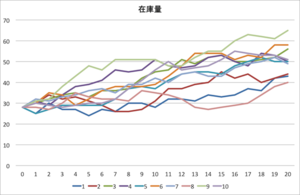
　また、気になる在庫ですが、ライン全体での在庫は、徐々に上昇することとなります。その振る舞いですが、１０回１０様でまさにばらつきました。２０日経過後の在庫量は、最小で４０最大で５６、平均５１となり、究極のコントロール環境での２８（４×７の初期在庫の維持）の約１．８倍となりました。

　次回は、同著で例としてあげている各工程の生産指示（に耐えうるキャパシティ）にばらつきを与えた状態でどんな振る舞いになったのかご紹介したいと思います。