ビルゲイツの面接試験に挑戦！

Life is beautifulにて「ビルゲイツの面接試験-－ジャンケン編」と言う

とっても興味深いエントリーがあったので、乗っかって見ます。

ルールはコチラ

引用－－－－－－－－－－－－－－－－－－－－－－－－－－

　あなた（＝Aさん）とBさんにジャンケンを連続で１０００回してもらいます。あなたもBさんも、パーで勝つたびに５００円、チョキで勝つたびに２００円 の賞金を主催者からもらえます。グーで勝ったり、アイコになった場合には一円ももらえません。この条件で、あなたの賞金を最大化するために、どんな戦略を 採りますか？ただし、Bさんと前もって相談することはできないし、試合中はしゃべったり身振りで合図を送ってはいけません。表情も見えないように、ミラー ガラスのヘルメットを被ってもらいます。試合中に見えるのは相手が何を出したかだけです。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－ココまで

うーん、答えはわからないので、俺の回答をば。

【正統派な回答編】
グーを出し続けて、Ｂさんにわざとパーで勝たせ続ける
おそらく最初の三回ぐらいは気がつかないことを考慮すると
残りの997回を勝たせるとして498,500円が
山分けできると考えられる。
よって最大利益は、249,250円

おそらく、まっとうに考えると上の答えが正しそうな感じだけども、
実は、違う気がするんですよね～。
まず、半分に分けるという前提がないから、
997回勝たせても利益を按分できる可能性が低いとか。
期待される最大値が500,000円のうち約半分の額までしか
稼ぐことができない点がどうにも引っかかりません。

その点を踏まえた上で再考

【利益の最大化前分析】
とりあえず、前提としてジャンケンの確立から
普通であれば出す確立は等しく33％のはずなんですが、
今回は条件があって
パーが500円
チョキが200円
グーが0円
あいこも0円
と言う仕組みが出来上がる。

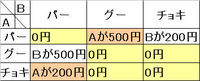
わかりやすく図にしてみる

ちょいとみずらいですがとりあえずオレンジのあたりじゃないと、

Aはお金がもらえないってわけですね。

グーを出しても期待値はゼロって言うヒントがありますが、

それを正攻法で解釈すると上のようになるわけですが、

うーん、難しい・・・だいぶ右脳っぽい回答になってしまいますが、

俺が考えた方法は以下のような感じです。

【利益の最大化作戦】

プランのテーマは
「常勝すると同時に、相手のロジックを壊す」
相手は、上の図に従うならば常にチョキを出すべきと言う結論に至るが、
それを、心理的な面で相手の心をひきつけるために
「相手よりも多く勝つ」と言う心理戦に持ち込む。

あくまで、「最大利益の追求」を念頭に置きながらも
相手と「ジャンケンによる勝負である」と言う土俵を作る。

よって、最初にジャンケンとして出すパターンとしては、
グー→チョキ→パーのパターンで、相手とジャンケンの勝負に持ち込む、
おそらく、10回ぐらいジャンケンを行えば、
相手は、一定の法則性があることに気がつくはず。
もう10回同じジャンケンパターンで行い、
相手を、グー→チョキ→パーに対して常勝させるロジックへと引き込む。

この時点で480回残っている。
ココからは、パターンを変える。
一定のパターンで勝ち続けてきたBは、ロジックが突然狂ったことで、
普通にじゃんけんをするようになる。

残り480回のジャンケンのうち、勝負がつかなかったの（あいこじゃなかった）が
3分の1と仮定して、-160で320回。
うち、均等に半分づつ勝ち負けをしたとして160勝することを想定。

480を過ぎた時点でグーとチョキとパーを出す割合を１：2：2で出すこととし、
160勝中、グーとチョキとパーの比率が1：2：2になると仮定。

32勝は、グーで勝ち無効なものとなる。
64勝は、チョキで勝ち200×64=12,800円
残りの64勝は、パーで勝ち500×64=32,000円

チョキの勝ちと、パーの勝ちをあわせて
44,800円となる・・・少ないなぁ・・・・

なにか他にいいアイディアあったらお教えください。
とりあえず自分の答えは44,800円です。