素数の秘密とリーマン予想

素数の本を一冊、休みに何の気なしに読んだら、はまってしまい、次々に読んでいます。

• 素数の音楽
• 素数に憑かれた人たち
• 興奮する数学

自分の整理のために、マインドマップにしてみます(拡大はこちら)。
http://wiki.esm.co.jp/Riemann.png
http://wiki.esm.co.jp/Riemann.pdf

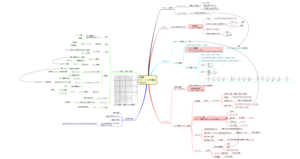ガウスが発見した、N以下の素数の数は、だいたいN/logN個という傾向（素数定理）から始まる素数の個数の研究が、オイラー積によって無限級数と出会い、リーマンのゼータ関数の零点問題へと進展したか、そしてそれがいかに現代の物理学や暗号理論と関係があるか、が主な関心事です。

ぼくは数学は好きでしたが、工学部だったからか数論は全く興味の対象外でした（今思うと惜しい）。解析や代数はよく勉強したつもりで、オイラーが無限級数を使うことで、指数関数の定義域を複素数に拡張したこと、また、その拡張が実に自然に三角関数と繋がっていくことを、計算過程としてファインマン物理学の教科書で（！）わくわく体験したのでした。そして、微積分の領域では、複素数の方が扱いやすい、というおもしろい傾向も。（微分可能＝積分可能）

ところが、オイラー積やゼータ関数については、最近まで知識がありませんでした。「２つの自然数が互いに素となる確率が6/π^2」という命題自身にびっくり（なぜπが!?）、さらにその証明でびっくり仰天。「エラトステネスのふるい」を代数的にやってしまったオイラー積に感動。（以下の説明がとっても読みやすくてクール）

http://www.sci.shizuoka.ac.jp/~math/math/contents/kiroku/Guide/zetaval2.pdf

さらに、このオイラー積の一般化であるゼータ関数に複素数を入れて考察すると、その零点が、N以下の複素数の数、と対数積分との「誤差」に関係してくる、という。

とってもわくわくして、この周辺を散歩した休日でした。