「倍返し」のリアル ~複利計算と「72」の法則~
»
こんにちは、今回もお読みいただきありがとうございます。
ドラマの半沢直樹が大人気ですね!主人公の半沢扮する堺雅人さんの演技は非常に真に迫るものがあります。
中でも流行しているのが「倍返しだ!」という決め台詞。
敵対する上司や国税庁、金融庁の役人を黙らせるカッコいいシーンですが、さすがに本当にあそこまでやる銀行員の方はいないだろうと思います。
しかし、実は「倍返し」そのものは、金融の世界では極々当たり前のように起こっているのです。というわけで、今回は複利計算について簡単におさらいをしてみます。
日本でお金を借りたり、あるいは預金したりする場合は、基本的に「利息」が発生します。例えば金利5%で120万円を借りた場合、1年間で6万円、ひと月で5,000円の利息が発生していくわけです。仮に利息も元金も支払わないままもう1年借り入れを続けると、もともと借り入れた120万円と、1年分の利息である6万円を加えた126万円に対して、5%の利息(63,000円)が生じます。
このような、「利息のそのまた利息」が発生する利息の計算方法を「複利計算」と言います。
そしてこの複利計算をしてみると、「倍返し」が意外と身近な存在だと言うことにも気づかされます。
くどいようですが、複利計算は「利息のそのまた利息」が生じる計算方法ですから、利率が高ければ高いほど、あるいは借り入れ期間が長ければ長いほど、支払うべき金額が大きくなっていきます。
借り入れ期間の長い融資の代表格と言えば住宅ローンですが、この住宅ローンは長ければ35年もの期間、分割払いを続けていくことになる契約です。
ローンを組むと、支払った金額の大半は利息・・・ということも珍しくありません。
それでは、実際に複利計算を行った場合、支払金額はどのように増えていくのでしょうか?ちょっと計算してみました。
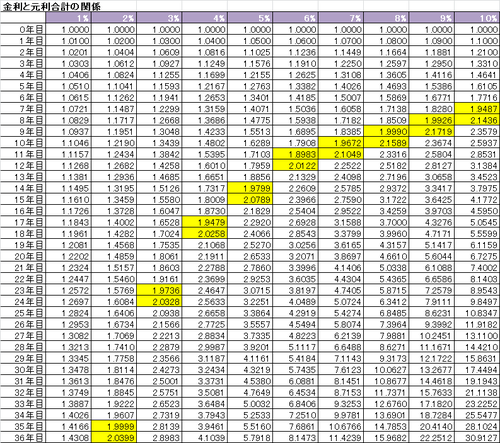
図はエクセルを使って複利計算を実施したものですが、簡単な覚え方として以下の計算式を頭に入れておくと、大きな借り入れをする場合には便利です。
元利金合計が借入金額の2倍になるまでに要する期間=72÷借入利率(%)
例えば1%で借り入れれば72年後、2%なら36年後、3%なら24年後・・・というように、72を利率で割った数が、概ね「倍返し」に要する期間です(図の黄色いマスが、「倍返し」のゾーンです)。
最近は住宅ローンの利率もずいぶん低いので、「倍返し」の事例も少なくなってはいますが、アベノミクスの効果で景気が回復したり、あるいは逆に国家財政が緊迫してきたりすると、金利が上昇する可能性が出てきます。
消費税の増税を前に住宅の駆け込み需要が一部で見られているようですが、ぜひ、税率だけでなく、利率にも気を配ってみてはいかがでしょうか??
SpecialPR