マックの裏メニューがトッピング100種類から100個まで自由に選べるとすると1.3那由他くらい組み合わせがあるのではないか?
日本マクドナルドが285通りの楽しみ方ができる“マックの裏メニュー”を始めるそうです。
“マックの裏メニュー”登場! 6月15日(水)から全国のマクドナルド店舗で期間限定販売
マクドナルド、定番バーガーに“裏メニュー” 285通りのオリジナルバーガーも
【前提となるルール】
- この285通りというのは3種類のトッピングから、最大3種類(1つ指定の場合の3通り、2つ指定の場合の6通り、3つ指定の場合の10通り)を足した19通りに、バーガー15種類を乗算することで285となるようです。
- このとき、2つ指定や3つ指定の場合に、同じものを重複して頼んでも良いルールです。(ハラペーニョの増し増し、スモークベーコンの増し増し増し、など)
- トッピング無しは考慮しません。
【基本となる計算方法】
その組み合わせの計算は、2種類や3種類の場合に同じものを重複して頼んでも良いルールのためいわゆるCombinationでなくてHomogenizationのほうで計算することになります。
とすると、式はこうなります。
 (1)
(1)
HomogenizationをCombinationに変換する公式
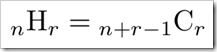 ・・・(2)
・・・(2)
がありますのでこれを当てはめると

単純に足し算部分を計算して

これくらいならば高校の数学で習ったとおりですがExcelに任せるとこうなります。combinというのはExcelの関数名です。
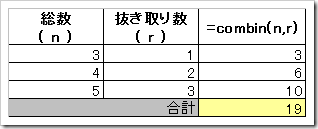
この19通りに対して元のバーガーの種類が15種類なので15*19=285通りというわけですね。
なお組み合わせが最大3つということでExcelでも3行+合計行の4行だけで済み、連続コピーを使えば簡単に計算できます。
ただこれがトッピング10種類やそれ以上となると面倒です。そんな時にこの公式を使ってみましょう。重複組合せの総和の公式です。
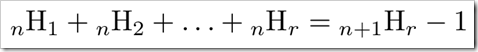 ・・・(3)
・・・(3)
これはn種類のトッピングから最大でr個まで重複を許して選んでも良い(ただし1つも選ばないというのはダメ)という意味の式となります。3種類(n=3)から3個まで(r=3)という条件ですと、(1)の式を経由せずとも(3)の式となり、(2)を当てはめればこのようになります。
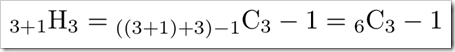
簡単すぎて嘘のようですが、以下の様にExcelのcombin関数で計算してみると

ということで、きちんと19となりました。(タイトル行のD-1列のDとはExcel上のD列の値である20から1引くことを意味しています。)
【条件の拡張その1 最大3つまでの制約あり】
あとは条件を変えてみたいと思います。オリジナルのトッピングで設定されているのはこの3種類。

「ピリリと辛いスライスしたハラペーニョ」

「濃厚なクリームチーズソース」

「香ばしい味わいのスモークベーコン」
これが4種類、5種類と増えたらどうなるでしょうか?
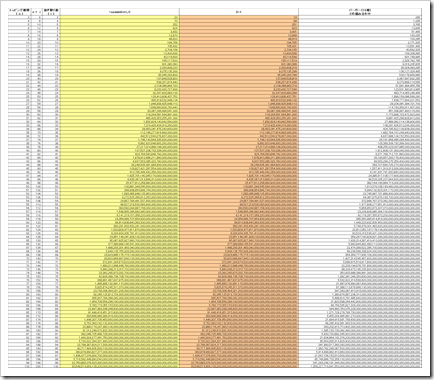
まずトッピングできるのが上限3個という条件を変えずにトッピング種類(n)の列だけを増やします。Excelで表を作るとこのようになりました。
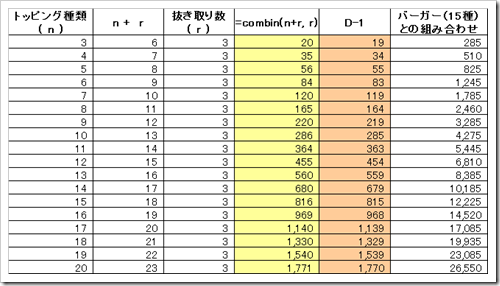
20種類まで増やしても、3個までしか選べない場合の重複組合せは2万6550通り(トッピングのみで1770通り)という範囲に収まっています。
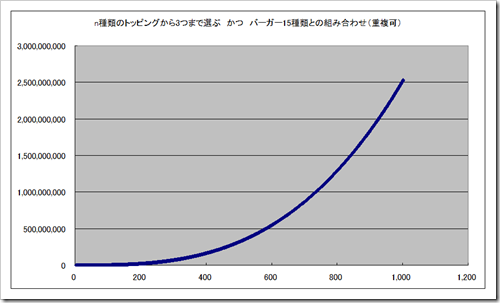
なお1000種類まで増やしたとしても2,515,027,500とのこと。25億通りですね。(トッピングのみで167,668,500通り)
【条件の拡張その2 トッピング個数はトッピングの種類と同じ数までOK】
ここまで考えると気になってくるのはひとつ。n種類のトッピングがあるのですから、消費者として選択する権利もn個まであるべきです。元の命題が3種類から3個までなのですからそれが当然の心理というものでしょう。4種類なら4個まで、5種類なら5個まで。野菜マシマシ・ニンニク・アブラ・カラカラ、ですとか、野菜マシマシマシマシマシが許容される世界です。(アブラ増し、などの1種類トッピングも依然としてOKです。)このとき表はnの列だけでなくrの列も増やしてこのように変わります。
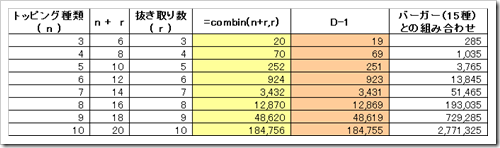
一番右の列から何か不穏な気配を感じます。まずトッピングをたったの5種類に増やした時点で3765通りのメニューが誕生しました。更に10種類まで増やすとには200万通りを超えています。プログラミング経験のある方ならO(オーダー)という概念を思い出されるかと思います。
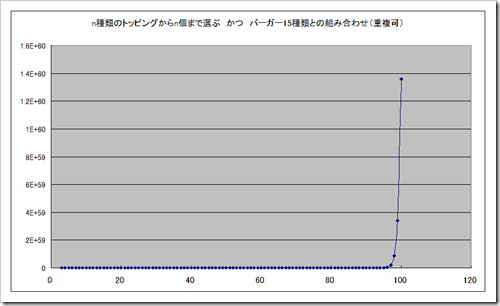
トッピングを100種類まで増やした計算をしてみましょう。すると、
1,358,227,719,841,550,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
通りということがわかりました。指数表記すると![]() ですかね。伝統的な単位に直すと1.358那由他(なゆた)になります。
ですかね。伝統的な単位に直すと1.358那由他(なゆた)になります。
↓は画像をクリックすると大きな画像が開きます。
もっと危険なOとなるとグラフがピーンと垂直に立つというよりも、Excelの桁のほうがピーンと伸びていくという危険さがあるようなのですが、私は幸いにしてそこまで計算量が爆発する様子を見たことがありません。
なお縦軸を対数としたグラフではこうなりました。
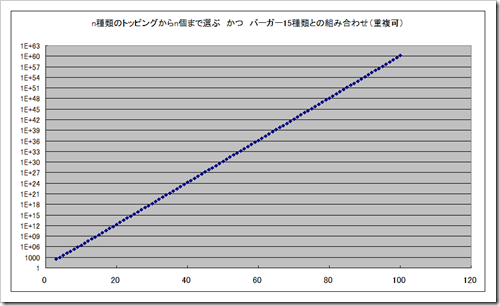
こういったコンピュータで取り組みたくない計算に、下のリンクのような問題もあるかと思います。
おねぇさぁぁぁぁぁん! 日本科学未来館のアニメに狂気が宿っていると話題に
これについては効率的なアルゴリズムがあるようでして、こういったところにコンピュータサイエンスの面白さがあるのかなと思いました。(小並感)
狂気の組み合わせ爆発を君も体験できる! 「おねえさんのコンピュータ」が登場
(もし誤りがあったら申し訳ありませんがどこかでご教示ください。)